Compressibility in Hydrostatic Systems

A comprehensive analysis of liquid compressibility and its significance in hydrostatic engineering and fluid mechanics

Introduction to Hydrostatic Principles

In the study of fluid mechanics, particularly within hydrostatic systems, understanding the behavior of liquids under various conditions is fundamental to engineering design and application. One of the key properties that influences liquid behavior in hydrostatic systems is compressibility. This property, often overlooked in basic fluid dynamics, plays a critical role in the performance and efficiency of hydraulic systems, lubrication mechanisms, and various other hydrostatic applications.

The following discussion delves into the scientific principles governing liquid compressibility, exploring its mathematical formulation, practical implications, and significance in hydrostatic engineering. By examining the relationship between pressure, volume, and the inherent properties of liquids, we can develop a comprehensive understanding of how compressibility affects system behavior and performance.

Fig. 1: Visual representation of liquid behavior under pressure in a hydrostatic system

Defining Liquid Compressibility

The property of a liquid that causes its volume to decrease under the action of pressure is known as compressibility. In hydrostatic systems, this property manifests when liquids are subjected to varying pressure conditions, affecting the overall system dynamics. Understanding this phenomenon is crucial for accurate modeling and prediction of hydrostatic system behavior.

For a liquid with volume V, when the pressure increases by Δp, the volume decreases by ΔV. In hydrostatic analysis, the relative change in volume per unit pressure change is a key parameter. This relationship forms the basis for quantifying compressibility in scientific and engineering applications.

In this formulation for hydrostatic analysis, the negative sign is introduced to ensure that k remains a positive value. This is necessary because pressure and volume changes in liquids typically exhibit an inverse relationship—when pressure increases (positive Δp), volume decreases (negative ΔV). Without this sign adjustment, the coefficient would inherently be negative, which contradicts the conventional understanding of compressibility as a positive property in hydrostatic contexts.

The volume compression coefficient k represents the fractional volume change per unit pressure change. In hydrostatic engineering, this parameter helps characterize how different liquids respond to pressure variations, enabling engineers to select appropriate fluids for specific applications based on their compressibility characteristics.

Bulk Modulus in Hydrostatic Systems

The reciprocal of the volume compression coefficient is known as the bulk modulus (K), a fundamental parameter in hydrostatic engineering. This property represents a liquid's resistance to compression, making it a critical factor in the design and analysis of hydraulic systems and other hydrostatic applications.

In hydrostatic terms, the bulk modulus K represents the pressure increment required to produce a unit relative volume change. This parameter is particularly important in hydraulic systems where pressure variations are common and system performance depends on predictable liquid behavior. A higher bulk modulus indicates a less compressible liquid, which is generally desirable in many hydrostatic applications to ensure system responsiveness and efficiency.

Under normal temperature conditions, pure hydraulic oil exhibits a bulk modulus K in the range of (1.4 to 2.0) × 10⁹ Pa. This relatively high value is why, in many practical hydrostatic applications, hydraulic oil is often considered incompressible. This simplifying assumption can be valid for basic system analysis and design, reducing computational complexity while still providing reasonably accurate results for many engineering purposes.

However, in precision hydrostatic systems or applications involving large pressure variations, the compressibility of hydraulic oil cannot be ignored. The small but finite compressibility can accumulate over large volumes or under extreme conditions, leading to significant system behavior deviations from incompressible assumptions.

Impact of Air Entrainment on Hydrostatic Performance

One critical factor affecting the compressibility of hydraulic fluids in hydrostatic systems is the presence of entrained air. Even small amounts of air can dramatically alter the compressibility characteristics of the liquid, with significant implications for system performance. This is because gases are inherently much more compressible than liquids, so their presence in a hydrostatic system creates a composite medium with substantially different properties than pure liquid.

When air becomes mixed with hydraulic oil, the resulting mixture's resistance to compression decreases markedly. This reduction in bulk modulus can lead to several undesirable effects in hydrostatic systems, including increased response time, reduced system stiffness, energy losses, and potential cavitation issues. In precision control applications, such as hydraulic positioning systems, these effects can compromise accuracy and performance.

The presence of air in hydraulic fluids is not the only factor influencing the effective compressibility in hydrostatic systems. The flexibility of the containers and piping that hold the liquid also plays a significant role. When pressure increases, these structures can expand slightly, effectively increasing the available volume and thus behaving similarly to increased liquid compressibility.

For accurate hydrostatic system analysis, engineers must consider the combined effects of: the inherent compressibility of the hydraulic oil, the compressibility of any entrained air, and the volumetric deformation of the containing structures. These combined effects are typically represented by an equivalent bulk modulus K', which accounts for all these factors in a single parameter.

In practical hydrostatic systems, the equivalent bulk modulus K' generally ranges from (0.7 to 1.4) × 10⁹ Pa, significantly lower than the bulk modulus of pure hydraulic oil. This reduction underscores the importance of considering these composite effects in system design and analysis.

The Hydraulic Spring Effect in Hydrostatic Systems

A fascinating and practically important manifestation of liquid compressibility in hydrostatic systems is the hydraulic spring effect. Under varying pressure conditions, the compressibility of hydraulic oil causes it to behave analogously to a mechanical spring. When pressure increases, the oil volume decreases, storing potential energy similarly to a compressed spring. Conversely, when pressure decreases, the oil volume expands, releasing stored energy—much like a spring returning to its natural state.

Fig. 3: Illustration comparing mechanical spring behavior with hydraulic spring effect in hydrostatic systems

This spring-like behavior has profound implications for hydrostatic system dynamics. When an external force change (ΔF) acts on a confined liquid, assuming the liquid's pressure-bearing area (A) remains constant, the length of the liquid column will change by Δl. This relationship forms the basis for understanding the hydraulic spring effect in hydrostatic systems.

The volume change (ΔV) resulting from this length change can be expressed as ΔV = AΔl, where A is the cross-sectional area. The corresponding pressure change (Δp) is given by Δp = ΔF/A, derived from the basic relationship between force, pressure, and area in hydrostatic principles.

This hydraulic spring effect is particularly significant in hydrostatic control systems, where it can influence system stability, response characteristics, and resonant frequencies. Engineers designing hydrostatic systems must account for this effect to avoid unexpected behavior, such as oscillations or delayed response times.

Calculating Hydraulic Spring Stiffness

In hydrostatic system analysis, the concept of hydraulic spring stiffness (Kₕ) is used to quantify the spring-like behavior of compressed liquids. Stiffness, in this context, refers to the force required to produce a unit displacement, analogous to the spring constant in mechanical systems. Understanding and calculating hydraulic spring stiffness is essential for predicting system dynamics in hydrostatic applications.

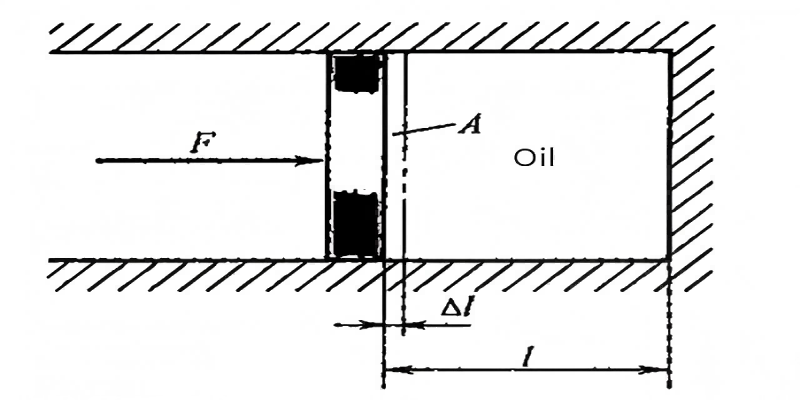
Fig. 2-1: Calculation of hydraulic spring stiffness in a confined liquid column

The hydraulic spring stiffness can be derived from the basic relationships between pressure, volume, and displacement in hydrostatic systems. By substituting the volume (V = Al, where l is the length of the liquid column) into the bulk modulus equation and relating force to pressure, we can develop an expression for stiffness.

This formula demonstrates that in hydrostatic systems, the hydraulic spring stiffness is directly proportional to the bulk modulus (K) and the cross-sectional area (A), while being inversely proportional to the length of the liquid column (l). This relationship has important implications for hydrostatic system design.

For example, increasing the cross-sectional area of a hydraulic cylinder in a hydrostatic system will increase its stiffness, making it more resistant to displacement under varying loads. Similarly, reducing the length of the hydraulic lines can increase system stiffness, which is why compact hydrostatic designs often exhibit more responsive behavior.

Understanding hydraulic spring stiffness is crucial for hydrostatic system engineers, as it directly affects system dynamics, stability, and performance characteristics. Proper calculation and consideration of this parameter ensure that hydrostatic systems behave predictably and meet design requirements.

Practical Implications in Hydrostatic Engineering

The compressibility of liquids and the resulting hydraulic spring effect have numerous practical implications in hydrostatic engineering. While the assumption of incompressibility simplifies many calculations, understanding when and how to account for compressibility is essential for designing efficient and reliable hydrostatic systems.

In hydrostatic systems where rapid pressure changes occur, such as in hydraulic impact tools or quick-acting valves, the compressibility of the fluid can lead to pressure transients or water hammer effects. These phenomena can cause noise, vibration, and even damage to system components if not properly accounted for in the design.

Another important application of hydrostatic compressibility principles is in the design of hydraulic damping systems. By carefully controlling the compressibility characteristics of the fluid, engineers can create effective damping mechanisms for absorbing shocks and vibrations in machinery and structures.

The selection of appropriate hydraulic fluids for specific hydrostatic applications also depends heavily on compressibility characteristics. In applications requiring high precision and responsiveness, fluids with higher bulk moduli (lower compressibility) are generally preferred, even if they come with other trade-offs in viscosity or lubricating properties.

Advanced Considerations in Hydrostatic Compressibility

While the basic principles of liquid compressibility in hydrostatic systems provide a foundation for understanding, several advanced considerations further refine our knowledge and application of these concepts. These factors, often overlooked in introductory treatments, can significantly impact system behavior in specialized applications.

Temperature plays a crucial role in the compressibility of liquids in hydrostatic systems. As temperature increases, most liquids exhibit a decrease in bulk modulus, meaning they become more compressible. This temperature dependence must be considered in hydrostatic systems operating over wide temperature ranges, such as those used in aerospace applications or industrial environments with extreme conditions.

Pressure itself can affect the bulk modulus of liquids in hydrostatic systems. For many liquids, the bulk modulus increases with pressure, meaning they become less compressible at higher pressures. This nonlinear relationship is particularly important in high-pressure hydrostatic systems, where the assumption of constant bulk modulus may lead to significant inaccuracies.

In hydrostatic systems with dynamic pressure variations, the frequency of pressure changes can also influence apparent compressibility. At very high frequencies, the relaxation time of molecular interactions in the liquid may become significant, leading to different effective bulk modulus values than those measured under static conditions.

For multi-phase flows in hydrostatic systems—where liquids coexist with gases or solids—the compressibility behavior becomes even more complex. The presence of multiple phases creates a composite material with compressibility characteristics that may vary significantly from the individual components, requiring advanced modeling techniques.

Recent advances in computational fluid dynamics (CFD) have enabled more accurate modeling of compressible flow in hydrostatic systems. These numerical techniques allow engineers to simulate complex flow behaviors, including the effects of compressibility, without relying solely on simplifying assumptions. This has led to more efficient and reliable hydrostatic system designs across various industries.

Conclusion: The Role of Compressibility in Hydrostatic Systems

The compressibility of liquids is a fundamental property with far-reaching implications in hydrostatic engineering and fluid mechanics. While the high bulk modulus of hydraulic oils allows for the simplifying assumption of incompressibility in many basic applications, a thorough understanding of compressibility effects is essential for advanced hydrostatic system design and analysis.

From the basic definition of volume compression coefficient to the practical implications of the hydraulic spring effect, the concepts explored in this discussion form the foundation for understanding liquid behavior under pressure in hydrostatic systems. Engineers and scientists working with hydraulic systems must appreciate both the theoretical formulations and practical considerations of liquid compressibility to develop effective, efficient, and reliable hydrostatic solutions.

The impact of air entrainment on compressibility, the calculation of hydraulic spring stiffness, and the various factors influencing bulk modulus all contribute to a comprehensive understanding of liquid behavior in hydrostatic systems. By mastering these concepts, professionals can optimize system performance, prevent failures, and innovate in the design of hydrostatic technologies.

As hydrostatic systems continue to evolve toward higher pressures, greater efficiencies, and more precise control, the importance of accurately modeling and understanding liquid compressibility will only increase. Future advancements in materials science, fluid dynamics, and system design will undoubtedly build upon these fundamental principles, pushing the boundaries of what is possible in hydrostatic engineering.