Pressure Loss in Fluid Flow
A comprehensive analysis of energy loss in fluid systems, with practical applications for hydraulic engineering and the hydraulic fluid tractor industry.

Introduction to Pressure Loss
Real fluids possess viscosity, which creates resistance when they flow. To overcome this resistance, flowing liquids must expend a portion of their energy. This energy loss is represented by the hg term in the Bernoulli equation for real fluids, as shown in equation (2-23). When converted to pressure loss, this can be expressed as Δp = ρghg.
In hydraulic systems, including the hydraulic fluid tractor, pressure loss converts hydraulic energy into heat, which can cause increased system temperature. Therefore, when designing hydraulic systems—whether for industrial machinery or a hydraulic fluid tractor—it is crucial to minimize pressure loss.
Pressure losses can be categorized into two main types: frictional pressure losses along pipelines and local pressure losses. Each type has distinct characteristics and calculation methods, which we will explore in detail. Understanding these losses is particularly important for optimizing the performance of a hydraulic fluid tractor, where efficiency directly impacts productivity and operating costs.
I. Frictional Pressure Losses
Frictional pressure loss refers to the pressure loss caused by viscous friction when fluid flows through straight pipes of constant diameter. The magnitude of this loss varies depending on the flow regime. In applications like the hydraulic fluid tractor, where efficient fluid transmission is critical, accurately calculating these losses ensures optimal system design.
A. Laminar Flow Frictional Losses
In laminar flow, fluid particles move in an orderly manner, allowing us to use mathematical methods to fully explore their flow conditions and derive formulas for calculating frictional pressure losses. This is particularly relevant for components of a hydraulic fluid tractor operating at lower speeds where laminar flow conditions prevail.
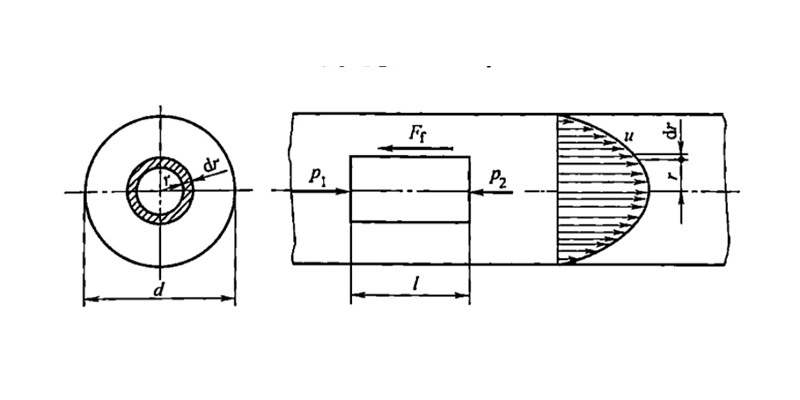
1. Velocity Distribution in Flow Cross-Section
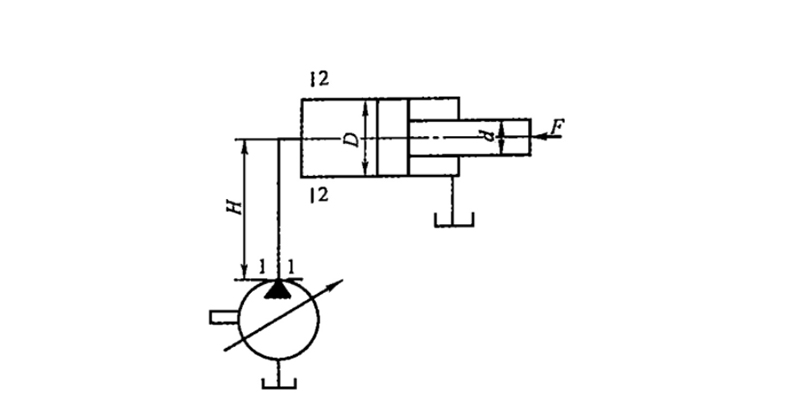
Consider the laminar flow of a hydraulic fluid tractor's operating fluid in a horizontal straight pipe of constant diameter, as shown in Figure 2-14. A small cylindrical element coinciding with the pipe axis is taken as the study object. Let its radius be r, length be l, the pressures acting on its two end faces be p₁ and p₂, and the internal friction force acting on its side surface be Ff.
When the fluid flows at a constant velocity, it is in a state of force equilibrium, so:
According to Newton's law of viscosity, Ff = -2πrlμ(du/dr) (the negative sign indicates that velocity u decreases as r increases). Letting Δp = p₁ - p₂ and substituting Ff into the above equation, we get:
Rearranging gives:
Integrating this equation and applying the boundary condition that u = 0 when r = R (where R is the pipe radius), we obtain:
This shows that the velocity of liquid particles in the pipe follows a parabolic distribution in the radial direction. The minimum velocity occurs at the pipe wall (r = R) where umin = 0, while the maximum velocity is at the pipe axis (r = 0) where umax = (Δp R²)/(4μl) = (Δp d²)/(16μl) (where d is the pipe diameter).
2. Flow Rate Through the Pipe
For a small annular flow cross-section with radius r and width dr, its area is dA = 2πrdr, and the flow rate through it is:
Integrating this from r = 0 to r = R gives:
3. Average Velocity in the Pipe
According to the definition of average velocity v, we have:
Comparing equation (2-29) with the maximum velocity umax, we find that the average velocity v is half of the maximum velocity umax.
4. Frictional Pressure Loss
Rearranging equation (2-29) gives the frictional pressure loss:
This shows that for laminar flow in straight pipes, the frictional pressure loss is proportional to the pipe length, flow velocity, and dynamic viscosity, and inversely proportional to the square of the pipe diameter. This relationship is crucial for designing efficient fluid transport systems, including those in a hydraulic fluid tractor.
Rewriting the equation in a more convenient form for practical calculations:
where λ is the friction coefficient. For laminar flow in circular pipes, the theoretical value is λ = 64/Re. However, considering possible deformation of the actual circular pipe cross-section and potential cooling of the liquid layer near the pipe wall, in practical calculations, λ = 75/Re for metal pipes and λ = 80/Re for rubber hoses commonly used in hydraulic fluid tractor systems.
Equation (2-30) was derived for horizontal pipes. Since the pressure changes caused by the self-weight of the liquid and positional changes are small and can be neglected, this formula also applies to non-horizontal pipes, such as those found in various orientations within a hydraulic fluid tractor.
B. Turbulent Flow Frictional Losses
The formula for calculating frictional pressure loss in turbulent flow has the same form as in laminar flow, i.e., Δpλ = λ (l/d) (ρv²/2). However, the friction coefficient λ in this case depends not only on the Reynolds number Re but also on the pipe wall roughness, expressed as λ = f(Re, Δ/d), where Δ is the absolute roughness of the pipe wall and Δ/d is the relative roughness.
For smooth pipes, λ = 0.3164Re-0.25. For rough pipes, the value of λ can be found from relevant charts in engineering handbooks based on different Re and Δ/d values. These charts are essential references for designing efficient hydraulic systems, including components of a hydraulic fluid tractor operating under turbulent conditions.
The absolute roughness of pipe walls varies with the pipe material. For general calculations, the following values can be referenced:
- Steel pipes: 0.04 mm
- Copper pipes: 0.0015~0.01 mm
- Aluminum pipes: 0.0015~0.06 mm
- Rubber hoses (common in hydraulic fluid tractor systems): 0.03 mm
Practical Note for Hydraulic Systems
In hydraulic fluid tractor design, selecting appropriate pipe materials and diameters based on expected flow conditions is critical. Turbulent flow generally creates higher pressure losses, so system designers often aim to maintain laminar or transitional flow regimes in critical components to improve efficiency and reduce operating costs.
II. Local Pressure Losses
Local pressure loss occurs when fluid flows through pipe elbows, fittings, sudden changes in cross-section, valve ports, filters, and other local devices. In these regions, the flow creates eddies and exhibits intense turbulence, resulting in significant energy loss. These components are numerous in a hydraulic fluid tractor, making local losses a major consideration in system design.
